- Research
- Open access
- Published:
Comparison of calculated and experimental power in maximal lactate-steady state during cycling
Theoretical Biology and Medical Modelling volume 11, Article number: 1 (2014)
Abstract
Background
The purpose of this study was the comparison of the calculated (MLSSC) and experimental power (MLSSE) in maximal lactate steady-state (MLSS) during cycling.
Methods
13 male subjects (24.2 ± 4.76 years, 72.9 ± 6.9 kg, 178.5 ± 5.9 cm,  : 60.4 ± 8.6 ml min−1 kg−1,
: 60.4 ± 8.6 ml min−1 kg−1,  : 0.9 ± 0.19 mmol l-1 s-1) performed a ramp-test for determining the
: 0.9 ± 0.19 mmol l-1 s-1) performed a ramp-test for determining the  and a 15 s sprint-test for measuring the maximal glycolytic rate (
and a 15 s sprint-test for measuring the maximal glycolytic rate ( ). All tests were performed on a Lode-Cycle-Ergometer.
). All tests were performed on a Lode-Cycle-Ergometer.  and
and  were used to calculate MLSSC. For the determination of MLSSE several 30 min constant load tests were performed. MLSSE was defined as the highest workload that can be maintained without an increase of blood-lactate-concentration (BLC) of more than 0.05 mmol l−1 min−1 during the last 20 min. Power in following constant-load test was set higher or lower depending on BLC.
were used to calculate MLSSC. For the determination of MLSSE several 30 min constant load tests were performed. MLSSE was defined as the highest workload that can be maintained without an increase of blood-lactate-concentration (BLC) of more than 0.05 mmol l−1 min−1 during the last 20 min. Power in following constant-load test was set higher or lower depending on BLC.
Results
MLSSE and MLSSC were measured respectively at 217 ± 51 W and 229 ± 47 W, while mean difference was −12 ± 20 W. Orthogonal regression was calculated with r = 0.92 (p < 0.001).
Conclusions
The difference of 12 W can be explained by the biological variability of  and
and  . The knowledge of both parameters, as well as their individual influence on MLSS, could be important for establishing training recommendations, which could lead to either an improvement in
. The knowledge of both parameters, as well as their individual influence on MLSS, could be important for establishing training recommendations, which could lead to either an improvement in  or
or  by performing high intensity or low intensity exercise training, respectively. Furthermore the validity of
by performing high intensity or low intensity exercise training, respectively. Furthermore the validity of  -test should be focused in further studies.
-test should be focused in further studies.
Introduction
Over the last 35 years, incremental graded exercise tests have been established for detecting endurance performance on the basis of a lactate-performance curve and the application of several different lactate-threshold concepts [1]. Most of these lactate concepts have the aim to approximate the power output achieved at maximal lactate-steady-state (PMLSS), which is one criterion of endurance performance [1, 2]. PMLSS is defined as the highest workload where lactate-formation and lactate-elimination in the muscle cell are maintained at a steady-state [2–4]. However, Hauser et al. [5] compared the power at "onset of blood lactate accumulation" (OBLA) [6, 7], the "individual anaerobic threshold" (IAT) [8] and the " + 1.5 mmol·l−1 lactate model" [9] with power in MLSS, measured during 30-minutes constant load tests. They found high significant correlations between OBLA and MLSS: r = 0.89 (mean difference −7.4 W); IAT and MLSS: r = 0.83 (mean difference 12.4 W), +1.5 mmol·l−1 lactate model and MLSS: r = 0.88 (mean difference −37.4 W). However, based on Bland-and-Altman, the comparison of power of all threshold-concepts with power in MLSS showed large individual differences, which deceive the high regression coefficients and small mean differences between these methods.
Furthermore, it is problematical that lactate-threshold concepts are based solely on the blood-lactate-concentration (BLC), which is mainly influenced by lactate formation, −transport, −diffusion and -elimination. Therefore, BLC may not represent the true metabolic processes occurring within the muscle cell. Mader [10, 11] and Bleicher et al. [12] have previously suggested that the same lactate-performance-curve may result from different combinations of maximal oxygen uptake ( ) and maximal lactate production rate (
) and maximal lactate production rate ( ). Furthermore, the shift of a lactate-performance curve could also be achieved by changing
). Furthermore, the shift of a lactate-performance curve could also be achieved by changing  or
or  separately.
separately.
Indeed, Bleicher et al. [12] verified, that two different athletes, (soccer and track), had exactly the same velocity for onset of blood lactate accumulation (OBLA) of 4.4 m s−1, yet the individual parameters of  and
and  were higher for the soccer player when compared to the track athlete (
were higher for the soccer player when compared to the track athlete ( : 70 vs. 63 ml min−1 kg−1;
: 70 vs. 63 ml min−1 kg−1;  0.93 vs. 0.65 mmol l−1 s−1, respectively). That confirms, therefore that identical MLSS could be originate by completely different combinations of
0.93 vs. 0.65 mmol l−1 s−1, respectively). That confirms, therefore that identical MLSS could be originate by completely different combinations of  - and
- and  -values. Using either
-values. Using either  ,
,  or BLC alone, it is not possible to explain differences of PMLSS between two athletes or the effects of training on the MLSS. As such, it would be beneficial to understand, how MLSS is controlled by glycolysis and oxidative phosphorylation within the muscle cell.
or BLC alone, it is not possible to explain differences of PMLSS between two athletes or the effects of training on the MLSS. As such, it would be beneficial to understand, how MLSS is controlled by glycolysis and oxidative phosphorylation within the muscle cell.
To explain the metabolic background of MLSS, Mader and Heck [3] introduced “A theory of the metabolic origin of anaerobic threshold”. The authors published a mathematical description of the metabolic response, based on measured values, exemplarily for a single muscle cell. They focussed on the activation of glycolysis (as the lactate production system) and on the oxidative phosphorylation (as the combustion system for lactate). Mader and Heck [3] argued that on the basis of Michaelis-Menten kinetics, it would be possible to calculate at the same time both, the rate of lactate-formation by glycolysis and its rate of lactate elimination by the oxidative phosphorylation, depending on a constant workload. These authors subsequently defined PMLSS as the crossing point at which the lactate-formation ( ) exactly equates to the maximal-elimination-rate of lactate (
) exactly equates to the maximal-elimination-rate of lactate ( ) as shown in Figure 1.
) as shown in Figure 1.
Presented are the parameters of “gross” lactate formation (
 ). The maximal elimination of lactate (
). The maximal elimination of lactate ( ) and maximal-lactate-steady-state (PMLSS) independence of
) and maximal-lactate-steady-state (PMLSS) independence of  steady-state (
steady-state ( ). All parameters are dictated by the
). All parameters are dictated by the  steady-state (Figure modified from Mader and Heck [3]).
steady-state (Figure modified from Mader and Heck [3]).
The present study, therefore, hypothesised firstly that it would be possible to calculate the PMLSS using the method by Mader and Heck [3] and secondly that knowledge of  and
and  (and their interaction) would help to better understand the mechanisms of the MLSS. These outcomes could provide a benefit compared to lactate-threshold concepts and to time-extensive 30 min constant-load tests.
(and their interaction) would help to better understand the mechanisms of the MLSS. These outcomes could provide a benefit compared to lactate-threshold concepts and to time-extensive 30 min constant-load tests.
Methods
Study sample
13 male subjects (age: 24.2 ± 4.76 yr, weight: 72.9 ± 6.9 kg, height: 178.5 ± 5.9 cm,  : 60.4 ± 8.6 ml·min−1·kg−1,
: 60.4 ± 8.6 ml·min−1·kg−1,  : 0.9 ± 0.19 mmol l-1 s-1) with different endurance levels participated in this study (training volume: n = 4 between 10 and 14 hours/week, n = 7 from 2 to 8 hours/week, n = 2 no sport). All subjects were informed about the aims of the study and subsequently provided written consent in accordance with the declaration of Helsinki [13].
: 0.9 ± 0.19 mmol l-1 s-1) with different endurance levels participated in this study (training volume: n = 4 between 10 and 14 hours/week, n = 7 from 2 to 8 hours/week, n = 2 no sport). All subjects were informed about the aims of the study and subsequently provided written consent in accordance with the declaration of Helsinki [13].
Procedure
All tests were performed on a Lode Excalibur Sport Ergometer (Lode, Groningen, NL). At the beginning of this investigation subjects performed, in a random order, a  test for detecting the maximal glycolytic rate and a
test for detecting the maximal glycolytic rate and a  test for detecting the maximal aerobic performance. Using the method introduced by Mader and Heck [3], PMLSSC was calculated on the basis of the individual
test for detecting the maximal aerobic performance. Using the method introduced by Mader and Heck [3], PMLSSC was calculated on the basis of the individual  ,
,  and body weight. PMLSSC was used for the first constant-load-test and several 30 min constant load-tests were undertaken to detect PMLSSE. Each test was performed on different days.
and body weight. PMLSSC was used for the first constant-load-test and several 30 min constant load-tests were undertaken to detect PMLSSE. Each test was performed on different days.
In order to detect  the subjects performed a sprint-test lasting 15 s which consisted of a 12 min warm-up period with a constant load set at 1.5 times of the individual body weight, followed by a second exercise bout with a constant load of 50 W for ten minutes. Directly after finishing the warm up phase, two blood samples were obtained from the earlobe in order to measure the lactate-concentration before the test. Following a countdown of 3 s the subjects began pedalling maximally in the seated position, with pedalling frequency being maintained at 130 rpm. The subjects had to retain the power output as long as possible. Blood samples were then immediately drawn and at every 60 s until the 9th min after the end of the test, to determine the maximum-post-exercise-lactate.
the subjects performed a sprint-test lasting 15 s which consisted of a 12 min warm-up period with a constant load set at 1.5 times of the individual body weight, followed by a second exercise bout with a constant load of 50 W for ten minutes. Directly after finishing the warm up phase, two blood samples were obtained from the earlobe in order to measure the lactate-concentration before the test. Following a countdown of 3 s the subjects began pedalling maximally in the seated position, with pedalling frequency being maintained at 130 rpm. The subjects had to retain the power output as long as possible. Blood samples were then immediately drawn and at every 60 s until the 9th min after the end of the test, to determine the maximum-post-exercise-lactate.  was calculated according to Equation 1 [14]:
was calculated according to Equation 1 [14]:

Equation 1: Calculation of maximal glycolytic rate.
Abbreviations are as follows: LamaxPost = Maximal Post Exercise Bloodlactate, LaPre = Bloodlactate before test, ttest = test duration = 15 sec, talac = alactic time interval
The alactic time interval (talac) was defined as the time from the beginning of the sprint (0 sec) to when the maximum power decreases by 3.5%.
Subjects performed a ramp-test for measuring  breath-by-breath (Oxycon Pro, Jäger, Höchberg, Germany) which included a warm up of 10 minutes at a constant load corresponding to 1.5 times of the participant’s body-weight, followed by a period of 2 min at a constant load of 50 W. The workload at the beginning of the test was set to 50 W for 2 min and was increased by 25 W every 30 s. The test was finished when subjects reached physically exhaustion, complaints of shortness of breath, dizziness or other physical complaints that unabled them proceeding the test [15].
breath-by-breath (Oxycon Pro, Jäger, Höchberg, Germany) which included a warm up of 10 minutes at a constant load corresponding to 1.5 times of the participant’s body-weight, followed by a period of 2 min at a constant load of 50 W. The workload at the beginning of the test was set to 50 W for 2 min and was increased by 25 W every 30 s. The test was finished when subjects reached physically exhaustion, complaints of shortness of breath, dizziness or other physical complaints that unabled them proceeding the test [15].  was calculated by the mean of all
was calculated by the mean of all  -values measured within the last 30s of the test.
-values measured within the last 30s of the test.
Calculation of PMLSSC
Step 1: Biochemical elementary background
In order to identify PMLSSC, the activity of glycolysis ( ) and oxidative phosphorylation (
) and oxidative phosphorylation ( ) must be known [3, 11]. Activation of
) must be known [3, 11]. Activation of  and
and  can be separately expressed by using the Michaelis-Menten kinetics (Equation 2) that is generally characterised by the activation of a single enzyme depending on a substrate and the maximal performance of glycolysis and oxidative phosphorylation, which is represented by
can be separately expressed by using the Michaelis-Menten kinetics (Equation 2) that is generally characterised by the activation of a single enzyme depending on a substrate and the maximal performance of glycolysis and oxidative phosphorylation, which is represented by  and
and  respectively. The KM which represents 50% of maximal activity rate must also be known.
respectively. The KM which represents 50% of maximal activity rate must also be known.

Equation 2: Elementary equation of Michaels-Menten-kinetics, where activation of an enzyme-substrate-complex ( ) depends on maximal performance (
) depends on maximal performance ( ), 50%-activity-constant (KM) and substrate (S).
), 50%-activity-constant (KM) and substrate (S).
It is mostly agreed that under nomoxic conditions the main regulating substrate (S) for the activation of  and
and  is the level of free ADP concentration [3, 11, 16, 17]. With an increase of the workload and therefore a higher demand of ATP, ADP-concentration rises exponentially within the muscle towards
is the level of free ADP concentration [3, 11, 16, 17]. With an increase of the workload and therefore a higher demand of ATP, ADP-concentration rises exponentially within the muscle towards  and
and  [11].
[11].
Step 2: Activation of oxidative phosphorylation (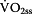 )
)
According to Mader [11] and Heck [3] can be assessed by using Hill equation (Equation 2) as a function of free ADP and
can be assessed by using Hill equation (Equation 2) as a function of free ADP and  . The 50%-activity-rate-constant of
. The 50%-activity-rate-constant of  (Ks1) is related to the exponent of ADP, which must be greater than 1.0 [3, 11, 18] otherwise it is not possible to calculate an appropriate activation of
(Ks1) is related to the exponent of ADP, which must be greater than 1.0 [3, 11, 18] otherwise it is not possible to calculate an appropriate activation of  [3, 11]. The exponent may reside in the range of 1.4 to 2 [17]. In the present paper an exponent of 2 was used, which leads to a 50% activity constant related to free ADP-concentration of 0.2512 mmol/kg of (0.2512)2 mmol/kg [3]. Therefore Ks1 was set to (ADP)2 = (0.2512)2 = 0.0631 [3, 19].
[3, 11]. The exponent may reside in the range of 1.4 to 2 [17]. In the present paper an exponent of 2 was used, which leads to a 50% activity constant related to free ADP-concentration of 0.2512 mmol/kg of (0.2512)2 mmol/kg [3]. Therefore Ks1 was set to (ADP)2 = (0.2512)2 = 0.0631 [3, 19].

Equation 3: Transformed equation of Michaels-Menten-kinetics to calculate the activation of oxidative phosphorylation ( ) – depending on maximal oxygen uptake (
) – depending on maximal oxygen uptake ( ), 50%-activity-constant (Ks1) and substrate (ADP).
), 50%-activity-constant (Ks1) and substrate (ADP).
Step 3: Activation of glycolysis (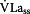 )
)
 mainly depends on the activation of the enzyme phosphofructokinase (PFK), which is activated by free ADP and AMP [3, 11, 18, 20]. AMP amplifies the activity of glycolysis in addition to ADP which leads to an exponent of 3 [3, 11]. Equation 4 describes the activation of
mainly depends on the activation of the enzyme phosphofructokinase (PFK), which is activated by free ADP and AMP [3, 11, 18, 20]. AMP amplifies the activity of glycolysis in addition to ADP which leads to an exponent of 3 [3, 11]. Equation 4 describes the activation of  as a function of free ADP and
as a function of free ADP and  . The 50%-activity-rate-constant of
. The 50%-activity-rate-constant of  (Ks2) due to PFK at ADP3 of 1.1 mmol/kg leads to Ks2 of 1.331 [3].
(Ks2) due to PFK at ADP3 of 1.1 mmol/kg leads to Ks2 of 1.331 [3].

Equation 4: Transformed equation of Michaels-Menten-kinetic to calculate the activation of glycolysis ( ) - depending on maximal glycolytic rate (
) - depending on maximal glycolytic rate ( ), 50%-activity-constant (Ks2) and substrate (ADP) (Figure 2).
), 50%-activity-constant (Ks2) and substrate (ADP) (Figure 2).
Steady-state activation and 50% activity rate of oxidative phosphorylation (
 , Ks1 = 0.0631) and glycolysis (
, Ks1 = 0.0631) and glycolysis (
 , Ks2 = 1.331). Data expressed as percentage of
, Ks2 = 1.331). Data expressed as percentage of  and
and  respectively, with respect to free ADP concentration (mmol/kgm). Modification from Mader and Heck [3].
respectively, with respect to free ADP concentration (mmol/kgm). Modification from Mader and Heck [3].
Step 4: Calculation of Lactate-elimination-rate depending on 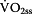
The oxidation of lactate primary occurs within the active muscle.  is a linear function (Equation 5) of the current
is a linear function (Equation 5) of the current  [3, 21]. Furthermore it not only depends on the amount of oxidized pyruvate/lactate per unit O2, which lies at 0.02049 mmol lactate/ml O2 but also on the distribution volume that was set to 0.4 in the present paper [3].
[3, 21]. Furthermore it not only depends on the amount of oxidized pyruvate/lactate per unit O2, which lies at 0.02049 mmol lactate/ml O2 but also on the distribution volume that was set to 0.4 in the present paper [3].

Equation 5: Calculation of maximal lactate elimination rate ( ) – depending on lactate equivalent, lactate distribution volume and activity of oxidative phosphorylation.
) – depending on lactate equivalent, lactate distribution volume and activity of oxidative phosphorylation.
However, there is no simple procedure to measure ADP-concentration and thus the activity rates of  and
and  in a daily endurance performance analysis. For an application of the model as a tool of endurance performance testing,
in a daily endurance performance analysis. For an application of the model as a tool of endurance performance testing,  and
and  must be calculated without measuring the free ADP-concentration. This is possible when the mentioned equations are transposed from ADP in
must be calculated without measuring the free ADP-concentration. This is possible when the mentioned equations are transposed from ADP in  depended equations.
depended equations.
Step 5: Transformation from ADP depended equations into  depended equations
depended equations
During training or testing,  can easily be measured by spirometry-devices or determined by a calculation (Equation 6), which is based on a linear function between
can easily be measured by spirometry-devices or determined by a calculation (Equation 6), which is based on a linear function between  and the workload [3].
and the workload [3].

Equation 6: Calculation for the activity of oxidative phosphorylation ( ) as dictated by workload (P) and bodyweight.
) as dictated by workload (P) and bodyweight.
If  is known or easily fit from 1 to
is known or easily fit from 1 to  , Equation 2 can be rearranged in Equation 7. Therefore ADP-concentration can be calculated for a special workload depending on
, Equation 2 can be rearranged in Equation 7. Therefore ADP-concentration can be calculated for a special workload depending on  and
and  , in the form of:
, in the form of:

Equation 7: Calculation of free ADP-concentration with respect to activated oxidative phosphorylation ( ) and maximal oxygen uptake (
) and maximal oxygen uptake ( ).
).
After replacing the term ADP in Equation 3 with the right term of Equation 7,  can be calculated as a function of
can be calculated as a function of  using Equation 8.
using Equation 8.

Equation 8: Calculation of glycolysis activity with respect to activated oxidative phosphorylation (VO2ss) and maximal glycolytic rate ( ).
).
Furthermore,  can also be calculated as demonstrated in Equation 5.
can also be calculated as demonstrated in Equation 5.
Step 6: Calculation of PMLSSC depending on 
The empirical determined values of  ,
,  and body weight are needed in order to calculate PMLSSC. MLSS is defined at the power at which lactate formation exactly equates to the maximal lactate elimination rate. Mathematically, this means
and body weight are needed in order to calculate PMLSSC. MLSS is defined at the power at which lactate formation exactly equates to the maximal lactate elimination rate. Mathematically, this means  . By using Equation 9,
. By using Equation 9,  in PMLSS can be calculated as:
in PMLSS can be calculated as:

Equation 9: Calculation in the activity of glycolysis with respect to the activation oxidative phosphorylation ( ) and maximal glycolytic rate (
) and maximal glycolytic rate ( ).
).
Only Equation 9 has to be used to calculate MLSS. However, there is no analytic solution for the calculation of  in Equation 9. Therefore, a numerical approximation such as the numerical interval bisection method or multiple mathematical optimized methods, has to be used, as implemented in computer software. If
in Equation 9. Therefore, a numerical approximation such as the numerical interval bisection method or multiple mathematical optimized methods, has to be used, as implemented in computer software. If  in PMLSSC could be determined, PMLSSC can be calculated by using Equation 10.
in PMLSSC could be determined, PMLSSC can be calculated by using Equation 10.

Equation 10: Calculation of power in MLSS (PMLSSC) depending on the activity of oxidative phosphorylation ( ), bodyweight and oxygen/workload-constant (Ks4).
), bodyweight and oxygen/workload-constant (Ks4).
Therefore the relation between  and power expressed as Ks4 must be known. In the present paper Ks4 was set to a constant value of 11.7 O2/W [3].
and power expressed as Ks4 must be known. In the present paper Ks4 was set to a constant value of 11.7 O2/W [3].
Constant load tests
Subjects performed at least two 30 min constant load exercise tests at a cadence of 70–80 rpm for determination the PMLSSE[2]. The first constant-load test according to PMLSSC started after a warm-up of 3 minutes at a power corresponding to 60% of the PMLSSC rate. Blood samples were taken during rest, after 4 and 8 min, and at subsequent 2 min intervals until the end of the test. The PMLSSE was defined as the highest workload that can be maintained without an increase of blood-lactate-concentration of more than 0.05 mmol·l−1·min−1 during the last 20 minutes of the test. Depending on blood-lactate-concentration, power in the next constant load test was set higher or lower by 10 W.
Statistical analysis
All data were analyzed using the software SPSS version 14. Descriptive statistics were calculated from the data (means, standard deviations (SD), minimum and maximum values). Normal distribution was verified using the Shapiro-Wilk-Test. Relationship between variables was investigated using orthogonal regression and correlation. The level of significance was set at α = 0.05 for all analyses.
Results
Descriptive values of  ,
,  , bodyweight, PMLSSC and PMLSSE are presented in Table 1. Furthermore, high significant correlation between PMLSSE and PMLSSC (r = 0.92; p < 0.001) (Figure 3) and PMLSSE and
, bodyweight, PMLSSC and PMLSSE are presented in Table 1. Furthermore, high significant correlation between PMLSSE and PMLSSC (r = 0.92; p < 0.001) (Figure 3) and PMLSSE and  (r = 0.84; p < 0.001) were found.
(r = 0.84; p < 0.001) were found.  shows no correlation with PMLSSE (r = −0.2; p > 0.05). The mean difference between PMLSSC and PMLSSE was 12 W ± 20 W.
shows no correlation with PMLSSE (r = −0.2; p > 0.05). The mean difference between PMLSSC and PMLSSE was 12 W ± 20 W.
Discussion
The aim of the present investigation was to compare the calculated and experimentally determined power output in MLSS. The comparison of PMLSSC and PMLSSE showed a highly significant correlation (0.92), with only a mean difference of 12 W ± 20 W between the two methods. The results of the present paper accords to previous comparisons between the different lactate-concepts and MLSS. It is well known that different lactate threshold concepts approximate in average MLSS rather well. Van Schuylenbergh et al. [22] published highly significant correlations between MLSS and OBLA and the Dmax method (r = 0.94 and r = 0.89, respectively). Heck [4] also evaluated correlations between MLSS and OBLA and individual anaerobic threshold of r = 0.92 and r = 0.87, respectively. However, as already mentioned, the investigation of Hauser et al. [5] showed large individual differences comparing power of threshold-concepts with power in MLSS. Therefore the calculation method is at least as useful the application of lactate-concepts to detect MLSS.
In contrast to lactate-concepts, however, by using the calculation method it is also possible to show the influence of individual  and
and  on MLSS, as well as their combined effects. This can be highlighted for subjects with similar
on MLSS, as well as their combined effects. This can be highlighted for subjects with similar  values, for example subject 5 and 12 at 61.0 and 62.7 ml·min−1·kg−1 respectively. Using the classical interpretation, endurance performance of these subjects would be nearly the same, yet interestingly PMLSSE of subject 5 and 12 were completely different (172 vs. 278 W). To explain this difference of 106 W, it is not possible to use only
values, for example subject 5 and 12 at 61.0 and 62.7 ml·min−1·kg−1 respectively. Using the classical interpretation, endurance performance of these subjects would be nearly the same, yet interestingly PMLSSE of subject 5 and 12 were completely different (172 vs. 278 W). To explain this difference of 106 W, it is not possible to use only  , but differences in
, but differences in  of both subjects (1.39 vs. 0.94 mmol·l−1·s−1) is also required. Therefore, subject 5 produces significantly more lactate within the muscle cell per second in contrast to subject 12. When related to the same
of both subjects (1.39 vs. 0.94 mmol·l−1·s−1) is also required. Therefore, subject 5 produces significantly more lactate within the muscle cell per second in contrast to subject 12. When related to the same  , this higher lactate production rate leads to a reduction of MLSS [10, 12].
, this higher lactate production rate leads to a reduction of MLSS [10, 12].
On the other hand it also seems pertinent to focus on subjects with the same PMLSSE, for example subject 5 and 13 (172 vs. 180 W). It is essential to mention that  and
and  values of these subjects are completely different (61 vs. 49 ml·min−1·kg−1 and 1.39 vs. 0.81 mmol·l−1·s−1, respectively). This particular example explains, why individuals with the same MLSS could originate by completely different combinations of
values of these subjects are completely different (61 vs. 49 ml·min−1·kg−1 and 1.39 vs. 0.81 mmol·l−1·s−1, respectively). This particular example explains, why individuals with the same MLSS could originate by completely different combinations of  and
and  as previously suggested by Bleicher et al. [12]. Therefore the knowledge of
as previously suggested by Bleicher et al. [12]. Therefore the knowledge of  and
and  and the application of the calculation method could help for a better interpretation of MLSS.
and the application of the calculation method could help for a better interpretation of MLSS.
Limitations
The reason for the overestimation of PMLSSC is likely caused by methodological as well as physiological aspects related to its calculation. It is well known, that a high positive correlation between  and PMLSS exists, which incidentally was confirmed in the present study, and highlights the importance of
and PMLSS exists, which incidentally was confirmed in the present study, and highlights the importance of  concerning PMLSS. The determination of
concerning PMLSS. The determination of  is a valid test procedure and well established in performance and clinical diagnostics [23]. However, Mader and Heck [3], Bleicher et al. [12], Heck and Schulz [14] and Mader [11] showed that on a theoretical basis,
is a valid test procedure and well established in performance and clinical diagnostics [23]. However, Mader and Heck [3], Bleicher et al. [12], Heck and Schulz [14] and Mader [11] showed that on a theoretical basis,  must have a significant influence on PMLSS. In the present investigation
must have a significant influence on PMLSS. In the present investigation  shows no correlation with PMLSSE, which was probably caused by the small range of
shows no correlation with PMLSSE, which was probably caused by the small range of  values measured in this investigation. Furthermore, the missing correlation between
values measured in this investigation. Furthermore, the missing correlation between  and PMLSSE as well as the overestimation of PMLSSC may have been caused by the methodological procedure in determining the maximal anaerobic performance. For example, in the present study
and PMLSSE as well as the overestimation of PMLSSC may have been caused by the methodological procedure in determining the maximal anaerobic performance. For example, in the present study  was measured by a sprint-test lasting 15 s. It is possible that testing
was measured by a sprint-test lasting 15 s. It is possible that testing  by using a test duration lower than 15 s would lead to higher maximal glycolytic rates and therefore on the basis of the same
by using a test duration lower than 15 s would lead to higher maximal glycolytic rates and therefore on the basis of the same  to a lower PMLSS [3, 12, 14]. Hauser [24] showed, that
to a lower PMLSS [3, 12, 14]. Hauser [24] showed, that  increases by 8% when measured using a 13 s sprint-test compared to a 15 s sprint-test. If the present
increases by 8% when measured using a 13 s sprint-test compared to a 15 s sprint-test. If the present  of 0.91 mmol·l−1·s−1 would be increased by 8%, the PMLSSC would have been 224 W. The bias between PMLSSC and PMLSSE would only be −7 W, which could from a practical point of view be neglected. Therefore test procedures of
of 0.91 mmol·l−1·s−1 would be increased by 8%, the PMLSSC would have been 224 W. The bias between PMLSSC and PMLSSE would only be −7 W, which could from a practical point of view be neglected. Therefore test procedures of  must receive greater focus in future investigations.
must receive greater focus in future investigations.
Another reason for the differences between the two methods could be the defined interval of 10 W between two constant-load tests, which was used because of time and economic reasons. Using the interval of 10 W it is possible, that PMLSSE is underestimated by a mean by 4 - 5 W. Consequently, it is possible that PMLSSE does not represent the PMLSS exactly. The possible increase of PMLSSE of 4 - 5 W would lead to a decrease in the difference between PMLSSC and PMLSSE of −7 W.
In addition, physiological reasons for differences could be based on the biological variability of the parameters and constants that were used in the calculation. As pointed out by Mader and Heck, the relation between  and power output (Ks4) has an important influence on PMLSS [3]. Again according to Mader and Heck [3] Ks4 was set to 11.7 O2/W in the present study. This relation corresponds exactly to the determined mean value of Ks4 used with the cycle ergometer. However, Ks4 varies on an interindividual basis [3], and only a theoretical increase of Ks4 by 2.5% would lead to a 224 W decrease in PMLSSC. In addition, the day-to-day variability of
and power output (Ks4) has an important influence on PMLSS [3]. Again according to Mader and Heck [3] Ks4 was set to 11.7 O2/W in the present study. This relation corresponds exactly to the determined mean value of Ks4 used with the cycle ergometer. However, Ks4 varies on an interindividual basis [3], and only a theoretical increase of Ks4 by 2.5% would lead to a 224 W decrease in PMLSSC. In addition, the day-to-day variability of  and
and  also has important influences on PMLSS, with a mean within-subject variation of 5.6% of
also has important influences on PMLSS, with a mean within-subject variation of 5.6% of  leading to deviations in PMLSSC of ± 30 W [25]. In contrast, the biological variability of
leading to deviations in PMLSSC of ± 30 W [25]. In contrast, the biological variability of  still remains unknown.
still remains unknown.
Conclusion
The mathematical method introduced by Mader and Heck [3] for the determination of PMLSS represents an accurate method similar to that of previous lactate-threshold concepts. In contrast to lactate-threshold concepts, however, this novel calculation method is based on  and
and  that can be used for explaining the origin of PMLSS and therefore the metabolic response. The knowledge of both parameters, as well as their individual influence on MLSS, could be important for establishing training recommendations, which could lead to either an improvement in
that can be used for explaining the origin of PMLSS and therefore the metabolic response. The knowledge of both parameters, as well as their individual influence on MLSS, could be important for establishing training recommendations, which could lead to either an improvement in  or
or  by performing high intensity or low intensity exercise training, respectively.
by performing high intensity or low intensity exercise training, respectively.
Ethical standards
The experiments comply with the current laws of the country. The study was proved by Ethics Commission.
Abbreviations
- ADP:
-
Adenosine diphosphate
- AMP:
-
Adenosine monophosphate
- ATP:
-
Adenosine triphosphate
- AT:
-
Anaerobic threshold
- BLC:
-
Blood-lactate-concentration
- BW:
-
Body weight
- CLarest :
-
Blood-lacate-concentration during rest
- CP:
-
Crossing point
- Dmax method:
-
Lactate threshold concept
- IAT:
-
Individual anaerobic threshold
- Ks1:
-
50%-activity constant of oxidative phosphorylation
- Ks2:
-
50%-activity constant of glycolysis
- Ks4:
-
Oxygen/workload equivalent
- MaxPostLa:
-
Maximum post excercise blood lactate concentration
- MLSS:
-
Maximal lactate-steady-state
- MLSSc:
-
Calculated maximal lactate steady-state
- MLSSE :
-
Experimental maximal lactat steady-state
- OBLA:
-
Onset of blood lactate accumulation
- PMLSS:
-
Power in maximal lactate-steady-state
- PMLSSC :
-
Power in calculated maximal lactate-steady-state
- PMLSSE :
-
Power in experimental maximal lactate-steady-state
- PFK:
-
Phosphofructokinase
- Pmax :
-
Maximal power
- rpm:
-
Revolutions per minute
- RER:
-
Respiratory exchange ratio
- SD:
-
Standard deviation
- talac :
-
Alactic time intervall
References
Heck H, Beneke R: 30 Years of Lactate Thresholds – what remains to be done? Dt Z Sportmed 2008, 59:297–302.
Beneke R: Methodological aspects of maximal lactate steady state-implications for performance testin. Eur J Appl Physiol 2003,89(1):95–99.
Mader A, Heck H: A theory of the metabolic origin of "anaerobic threshold". Int J Sports Med 1986,7(1):45–65.
Heck H: Laktat in der Leistungsdiagnostik. Schorndorf: Hofmann; 1990.
Hauser T, Adam J, Schulz H: Comparison of selected lactate threshold parameters with maximal lactate‒steady‒state in cycling. Int J Sport Med 2013. Epub ahead of print
Jones AM, Doust JH: The validity of the lactate minimum test for determination of the maximal lactate steady state. Med Sci Sports Exerc 1998,30(8):1304–1313.
Sahlin K, Harris RC, Nylind B, Hultman E: Lactate content and pH in muscle obtained after dynamic exercise. Pflugers Arch 1976,367(2):143–149.
Sjödin B, Jacobs I: Onset of blood lactate accumulation and marathon running performance. Int J Sports Med 1981,2(1):23–26.
Dickhuth H-H, Yin L, Niess A, Röcker K, Mayer F, Heitkamp HC, Horstmann T: Ventilatory, lactate-derived and catecholamine thresholds during incremental treadmill running: relationship and reproducibility. Int J Sports Med 1999,20(2):122–127.
Mader A: Eine Theorie zur Berechnung der Dynamik und des steady state von Phosphorylierungszustand und Stoffwechselaktivität der Muskelzelle als Folge des Energiebedarfs. Köln: Dt. Sporthochschule; 1984.
Mader A: Glycolysis and oxidative phosphorylation as a function of cytosolic phosphorylation state and power output of the muscle cell. Eur J Appl Physiol 2003,88(4–5):317–338.
Bleicher A, Mader A, Mester J: Zur Interpretation von Laktatleistungskurven - experimentelle Ergebnisse mit computergestützten Nachberechnungen. Spectrum der Sportwissenschaften 1998, 10:92–104.
Harriss DJ, Atkinson G: Update–Ethical standards in sport and exercise science research. Int J Sports Med 2011,32(11):819–821.
Heck H, Schulz H: Diagnostics of anaerobic power and capacity. Dt Z Sportmed 2002, 53:202–212.
Mader A, Liesen H, Heck H, Phillipi H, Rost R, Schürch P, Hollmann W: Zur Beurteilung der sportartspezifischen Ausdauerleistungsfähigkeit im Labor. Dt Z Sportmed 1976, 27:80–88. 109–112
Chance B, Williams GR: Respiratory enzymes in oxidative phosphorylation. I. Kinetics of oxygen utilization. J Biol Chem 1955,217(1):383–393.
Mader A, Heck H: Energiestoffwechselregulation, Erweiterungen des theoretischen Konzepts und seiner Begründungen. Nachweis der praktischen Nützlichkeit der Simulation des Energiestoffwechsels. In Brennpunktthema Computersimulation: Möglichkeiten zur Theoriebildung und Ergebnisinterpretation. Edited by: Mader A, Allmer H. Sankt Augustin: Academia-Verl; 1996:124–162.
Newsholme EA, Start C: Regulation in metabolism. London: Wiley & Sons; 1973.
Barstow TJ, Buchthal SD, Zanconato S, Cooper DM: Changes in potential controllers of human skeletal muscle respiration during incremental calf exercise. J Appl Physiol 1994,77(5):2169–2176.
Krause U, Wegener G: Control of adenine nucleotide metabolism and glycolysis in vertebrate skeletal muscle during exercise. Experientia 1996,52(5):396–403.
Donovan CM, Brooks GA: Endurance training affects lactate clearance, not lactate production. Am J Physiol 1983,244(1):83–92.
Van Schuylenbergh R, Vanden Eynde B, Hespel P: Correlations Between Lactate and Ventilatory Thresholds and the Maximal Lactate Steady State in Elite Cyclists. Int J Sports Med 2004,25(06):403–408.
Weltman A, Snead D, Stein P, Seip R, Schurrer R, Rutt R, Weltman J: Reliability and Validity of a Continuous Incremental Treadmill Protocol for the Determination of Lactate Threshold, Fixed Blood Lactate Concentrations, and V̇O 2max . Int J Sports Med 1990,11(01):26–32.
Hauser T: Untersuchungen zur Validität und Praktikabilität des mathematisch bestimmten maximalen Laktat-steady-states bei radergometrischen Belastungen [abstract]. TU-Chemnitz: Chemnitz; 2012.
Katch VL, Sady SS, Freedson P: Biological variability in maximum aerobic power. Med Sci Sports Exerc 1982,14(1):21–25.
Acknowledgements
The authors would like to thank Steffi Hallbauer and Jörg Kersten for their assistance in the laboratory and Scott Bowen for their help.
Funding
The publication coast of this article were founded by the German Research Foundation/DFG (Geschäftszeichen INST 270/219-1) and the Chemnitz University of Technology in the funding programme Open Access Publishing.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interest
The authors declare that they have no conflict of interest.
Authors’ contributions
Data collection: TH, JA, Manuscript: TH, JA, HS. All authors read and approved the final manuscript.
An erratum to this article can be found at http://dx.doi.org/10.1186/s12976-016-0044-3.
Rights and permissions
This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Hauser, T., Adam, J. & Schulz, H. Comparison of calculated and experimental power in maximal lactate-steady state during cycling. Theor Biol Med Model 11, 1 (2014). https://doi.org/10.1186/1742-4682-11-25
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1742-4682-11-25




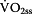 )
)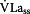 )
)
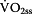
 depended equations
depended equations
